Hemi Nae
Hydan Technologies, Inc.
Princeton Junction, New Jersey, United States
*Grow with the Flow is a Trademark of Hydan Technologies, Inc.
July 15, 2016

Cosmetic chemists aim to formulate complex, balanced, stable, and safe products that are easy to apply and provide the consumer with optimal application properties. Whether the product is a shampoo, a skin care cream, an oral care formulation, a nail polish, or a lipstick, it is made of a complex mixture of raw materials that form a three-dimensional complex fluid structure. Cosmetic formulations must withstand various conditions during their life cycle:
1. During formulation and production, which we refer to as the construction stage, in which the three-dimensional structure of the product is formed;
2. While sitting on a store shelf, or at the consumer's house, the maintenance stage, in which the three-dimensional complex structure has to remain stable over time;
3. During application—the demolition stage—in which the consumer applies an external force to break down the three-dimensional structure of the product and enables it to flow;
4. Following application, a recovery stage—the reconstruction stage—where the product tries to restore its original three-dimensional structure.
We follow these changes and compare the flow properties of cosmetic formulations using the principles of rheology—the science dealing with how materials deform and flow under the influence of external forces, including gravity. The name rheology comes from the Greek word rheo (= flow). In 1929, Marcus Reiner and Eugene Bingham proposed the formation of a “new” scientific discipline utilizing the same name.1 They were inspired by a quotation attributed to Heraclitus: “Everything Flows” (in Greek: "Panta Rhei"). However, studies of the rheological properties of flowing systems date back to Archimedes (~250 BC), Hooke (1678), Newton (1687), Stokes (1845), Maxwell (1867), Boltzman (1878), Einstein (1906), Trouton (1906), and others.2 Characterization of the rheological properties of a system, and understanding the interaction of the various ingredients that build up the complex structure of cosmetic products is critical since it reveals why the system behaves the way it behaves under various conditions and leads to the required modifications needed to formulate new and improved products.
We may imagine the product as a certain volume of material that occupies the space between two plates. The material is moving in a certain direction due to an external force (F). At rest, the material has a thickness (x0), length (l0) and width (w0). Assuming that the bottom plate is stationary and the flow is laminar, the upper plate is displaced by dl and the thickness by dx as shown in Figure 1.
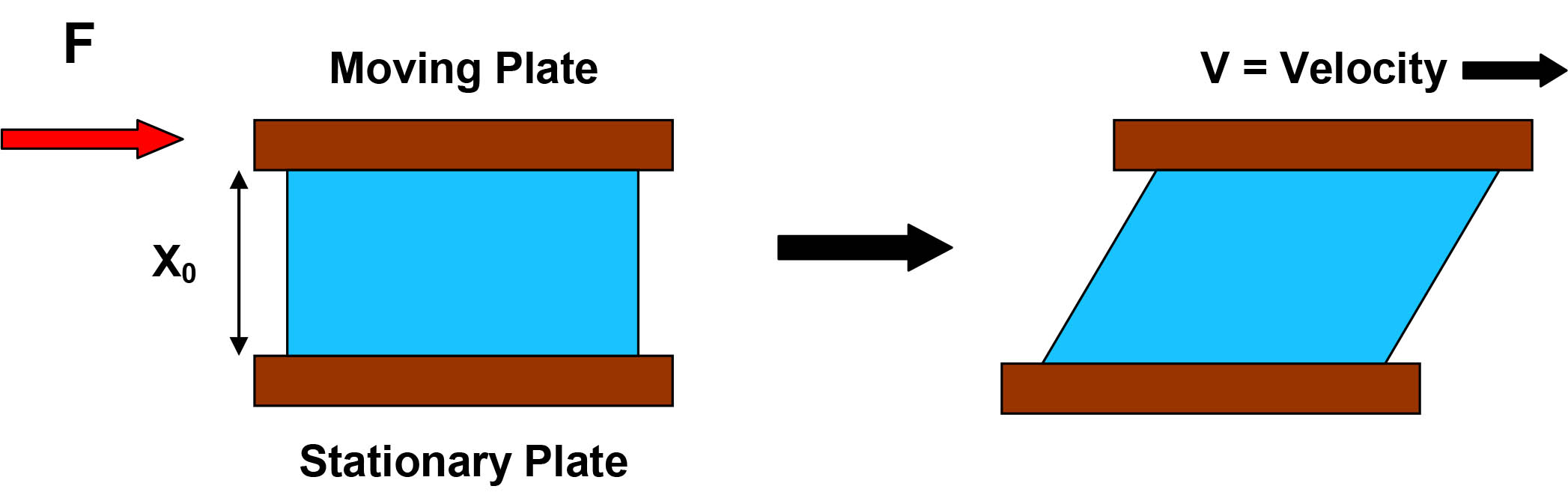
Figure 1: Basic model of flow between two plates.
The ratio of the external force (F) to the affected area (A) is defined as the shear stress (σ):
σ = F/A
The shear strain (γ) is defined as the relative change in the length of the material due to the external force:
γ = l/l0
The ratio between the shear stress (σ) and the shear strain (γ) is defined as the modulus (G):
G = σ/ γ
If the top plate in Figure 1 is moving at a certain velocity (v), the velocity gradient dv/dx is defined as the shear rate (γ̇). Sir Isaac Newton, who formulated the laws of motion and universal gravitation, discovered that in ideal fluids (known as Newtonian fluids), the shear stress (σ) is directly related to the shear rate (γ̇):
σ = ηγ̇ or η = σ/γ̇
Newton concluded that this ratio (η), the viscosity, is: "The resistance which arises from the lack of slipperiness originating in a fluid—other things being equal—is proportional to the velocity by which the parts of the fluid are being separated from each other."3 The viscosity of Newtonian Fluids is therefore constant and is independent of the shear rate. Most fluid systems, however, are not Newtonian (known as non-Newtonian fluids) and their viscosity is not constant, but changes as a function of increasing or decreasing the applied shear rate. Many fluids show a decrease in viscosity as a function of increasing shear rate. These fluids are called pseudoplastic fluids. The “structure” of the fluid in these systems is broken down due to the external force, resulting in a shear thinning behavior. If the initial inter-particle (or molecular) association is strong, the system may behave like a solid at rest. The initial shear stress that is required to overcome the internal forces and disrupt the structure is defined as the yield value of the system. Materials that exhibit a yield value and then demonstrate shear thinning with increasing shear rate are defined as plastic fluids. Some fluids exhibit an increase in viscosity with increasing shear rate, a phenomenon known as shear thickening. These materials are defined as dilatant fluids. We may compare the flow behavior of various systems by plotting either the shear stress as a function of shear rate as shown in Figure 2a or the viscosity as a function of shear rate as shown in Figure 2b.
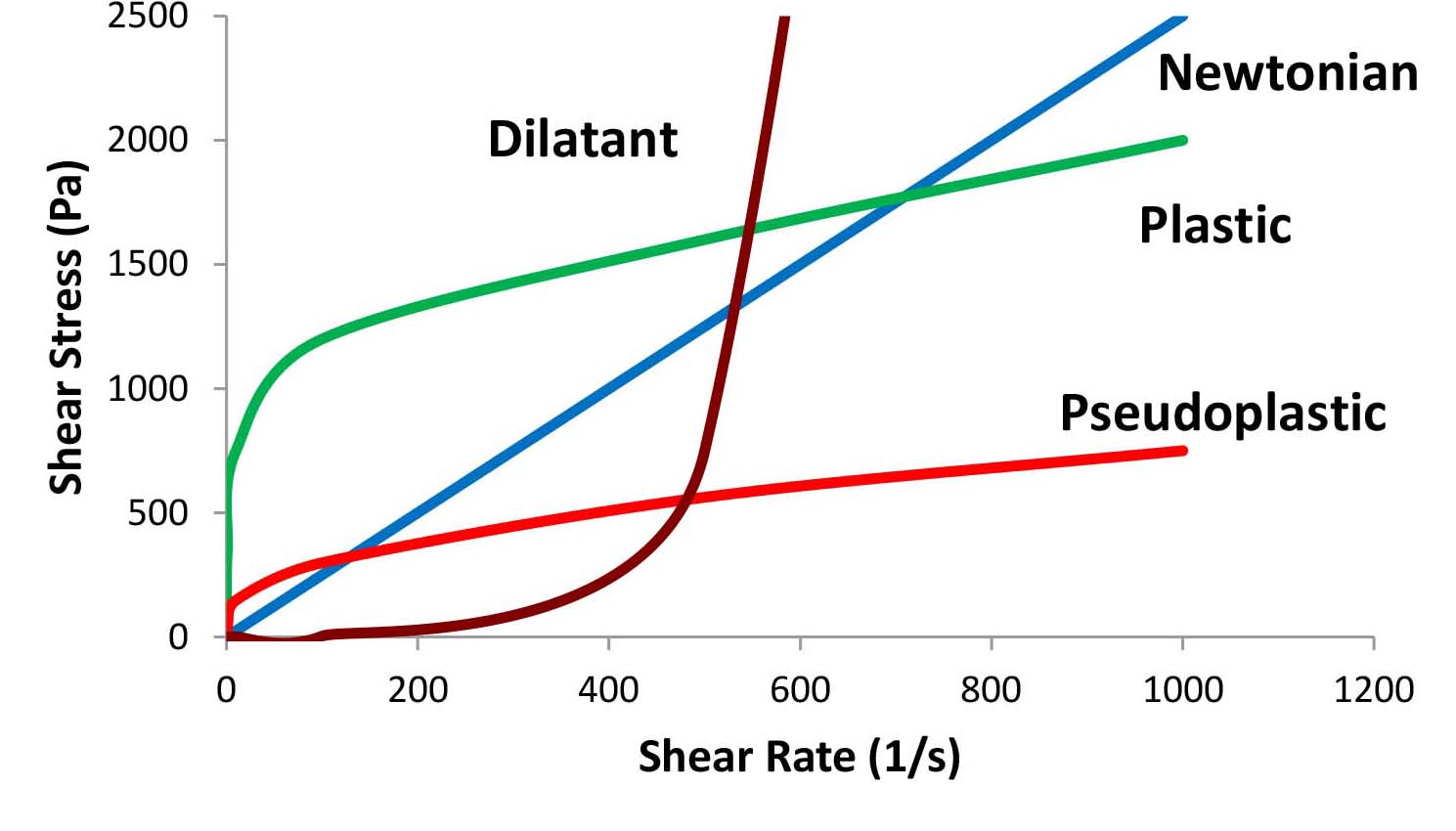
Figure 2a: Shear stress as a function of shear rate (Note: linear-linear scale).
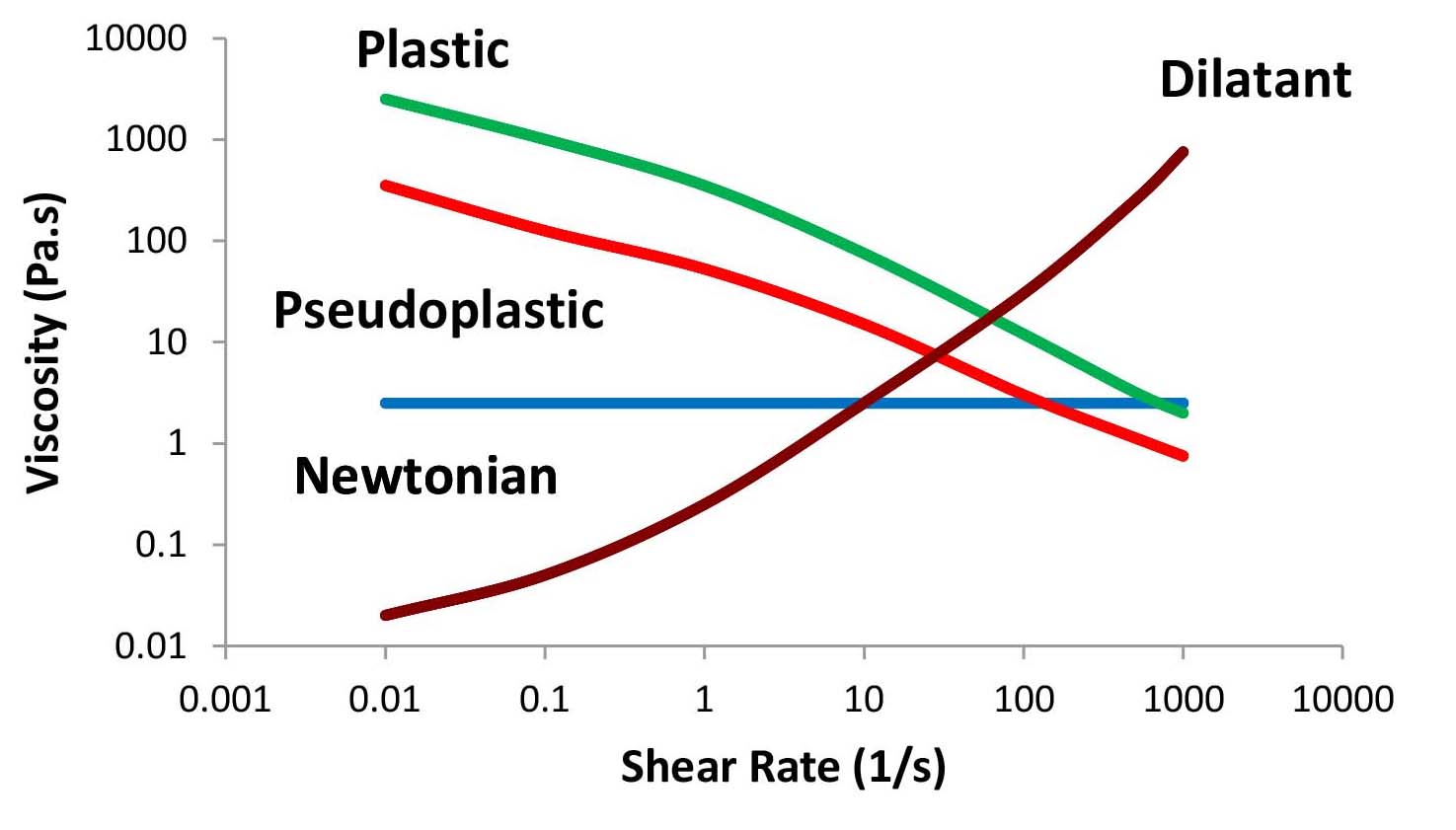
Figure 2b: Viscosity as a function of shear rate (Note: log-log scale).
Figures 3a and 3b show the flow profiles of two formulations that exhibit the same viscosity at a certain shear rate (about 70 1/s) but behave differently when applied. In Figure 3a, we monitor viscosity as a function of shear rate, while viscosity as a function of shear stress is plotted in Figure 3b. The viscosity of system A is higher at low shear rates while the viscosity of system B is higher at high shear rates. These differences may be detrimental to the flow behavior of the product during the four stages discussed above.
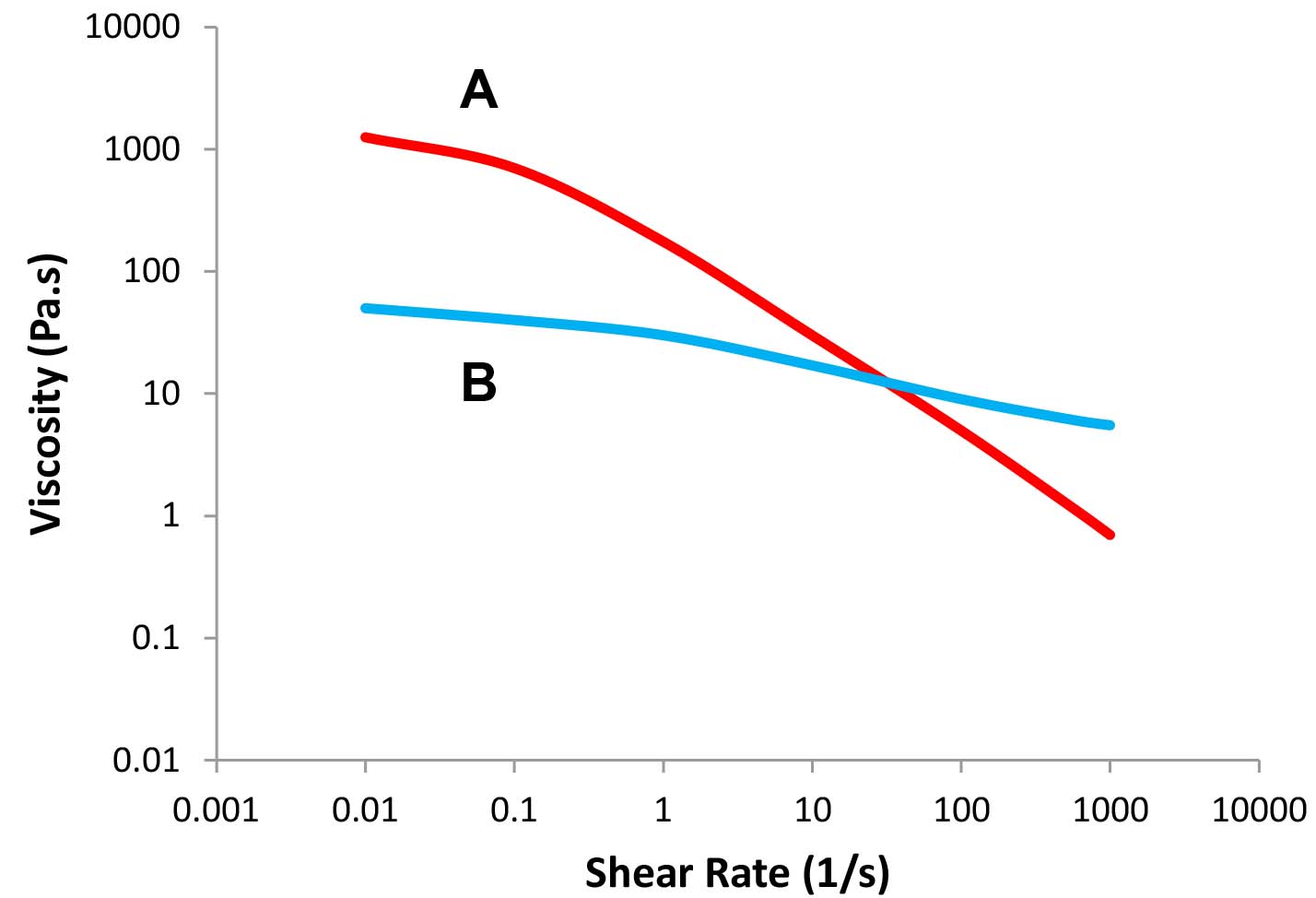
Figure 3a: Viscosity as a function of shear rate – Formulas A and B
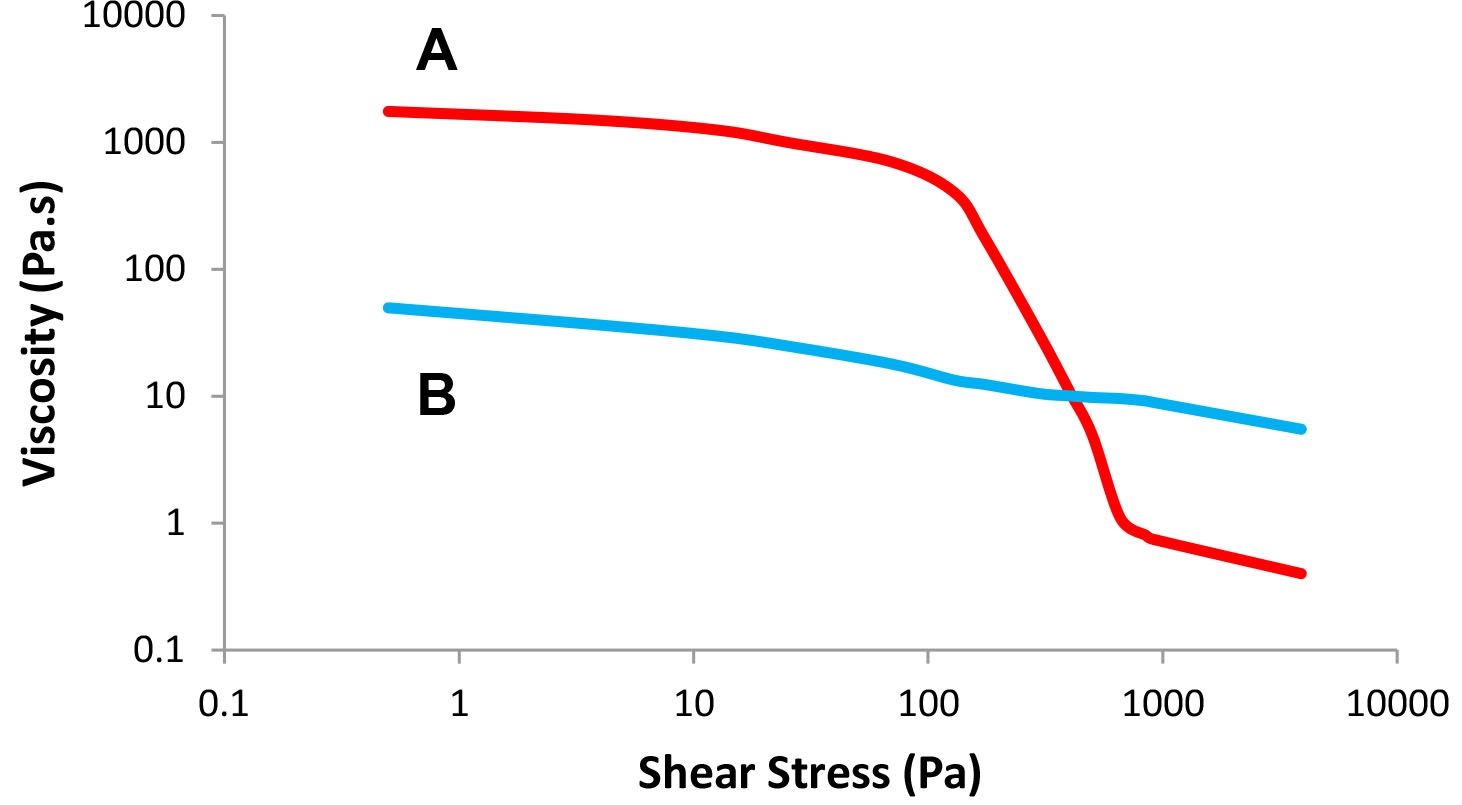
Figure 3b:
Viscosity as a function of shear stress – Formulas A and B
When we measure the properties of a cosmetic formulation, we have to ensure that the time scale of the system is faster than the time scale of the observation/test. If we measure changes that take a very long time, our experiment should run a very long time. The ratio of the time scale of the system (tc)—the stress relaxation time—to the time scale of the observation (tp) was defined by M. Reiner based on a line from Deborah’s song “The mountains flowed before the Lord” (Judges 5:5), as the Deborah Number:1
De = tc/tp
An example of the importance of the time scale of the experiment is the pitch drop experiment at Queensland University, Australia, which has been recorded in the Guinness World Records as the world’s longest running laboratory experiment.4
In order to describe the state of a complex fluid we look at a specific volume of the material and describe the relationship between some physical properties that are specific to the material, such as stress and strain. A typical general equation that describes the state of the fluid is called the Constitutive Equation. It is usually expressed as an array of components (Tensors) that are functions of the coordinates of a certain space. Thus, the Stress Tensor Element (Tik) depends on the strain or the strain rate and time. Examples of simple general constitutive equations of Non-Newtonian fluids are the Reiner-Rivlin equation and the KBKZ (Kaye-Bernstein, Kearsley, Zapas) equation.5-7
When an external force is removed, a complex fluid rearranges, trying to restore its initial network structure over a period of time. Therefore, viscosity should be measured not only as a function of increasing shear rate while the structure is broken down but also as a function of decreasing shear rate while the system recovers its structure. This phenomenon is known as the hysteresis effect. If the recovery is fast, the plot of viscosity as a function of decreasing shear rate would be superimposed on the plot of viscosity as a function of increasing shear rate. However, it may take time for the fluid to restore its structure and therefore the “down curve” would be below the “up curve” as shown in Figure 4. We define thixtropy as the ability of the system to exhibit shear thinning with increased shear rate and slower recovery with decreasing shear rate. If the "up" and "down" curves overlap, the material is called non-thixotropic and if the "down" curve is above the "up" curve, the material is called rheopectic.
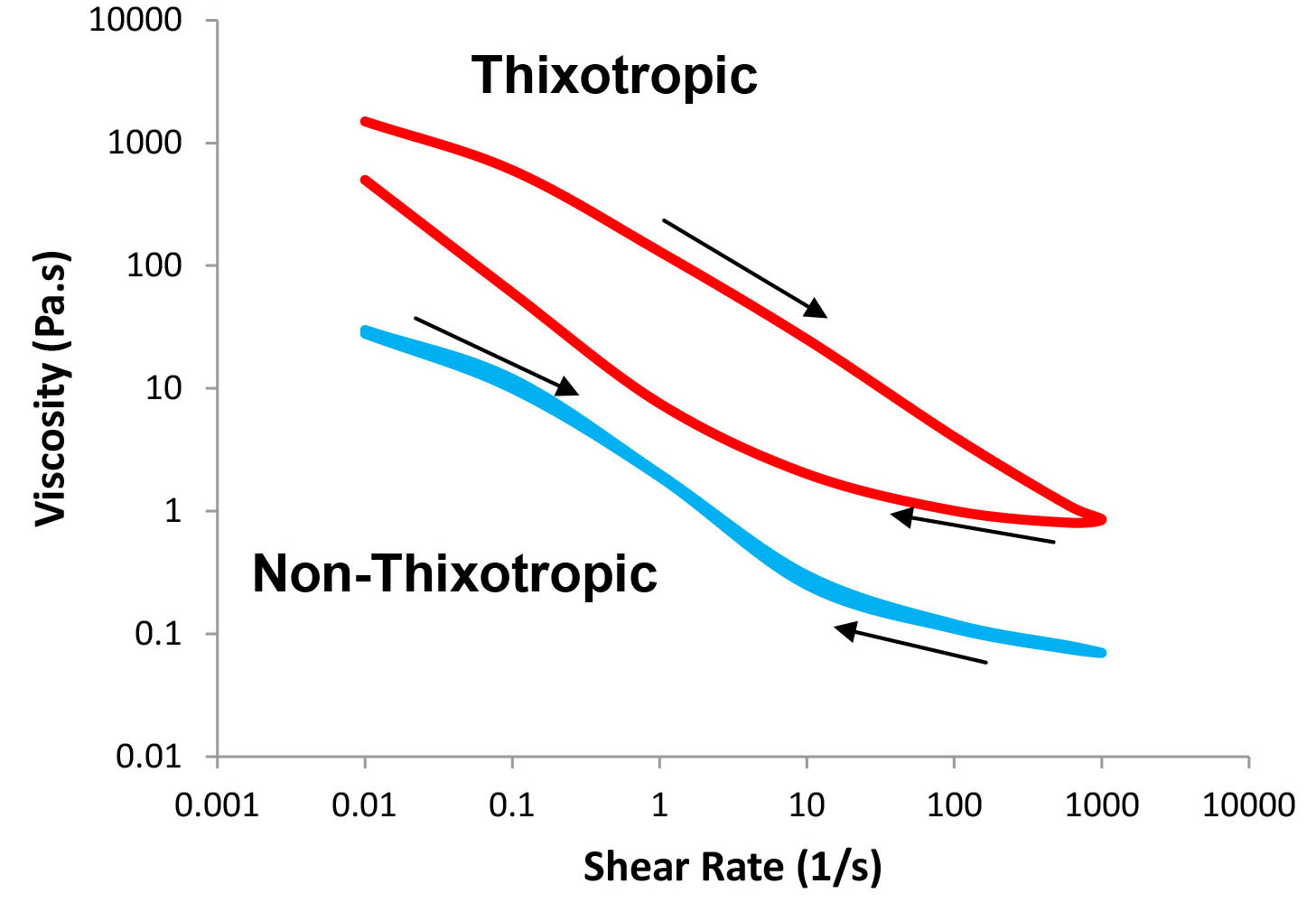
Figure 4: Viscosity as a function of shear rate – thixotropic and non-thixotropic behavior (arrows show increasing or decreasing shear rate).
Another way to evaluate how the system rebuilds its network structure is to follow the decrease in viscosity at a constant shear rate as the structure is being broken down, followed by the recovery of viscosity at a much lower shear rate as shown in Figure 5.
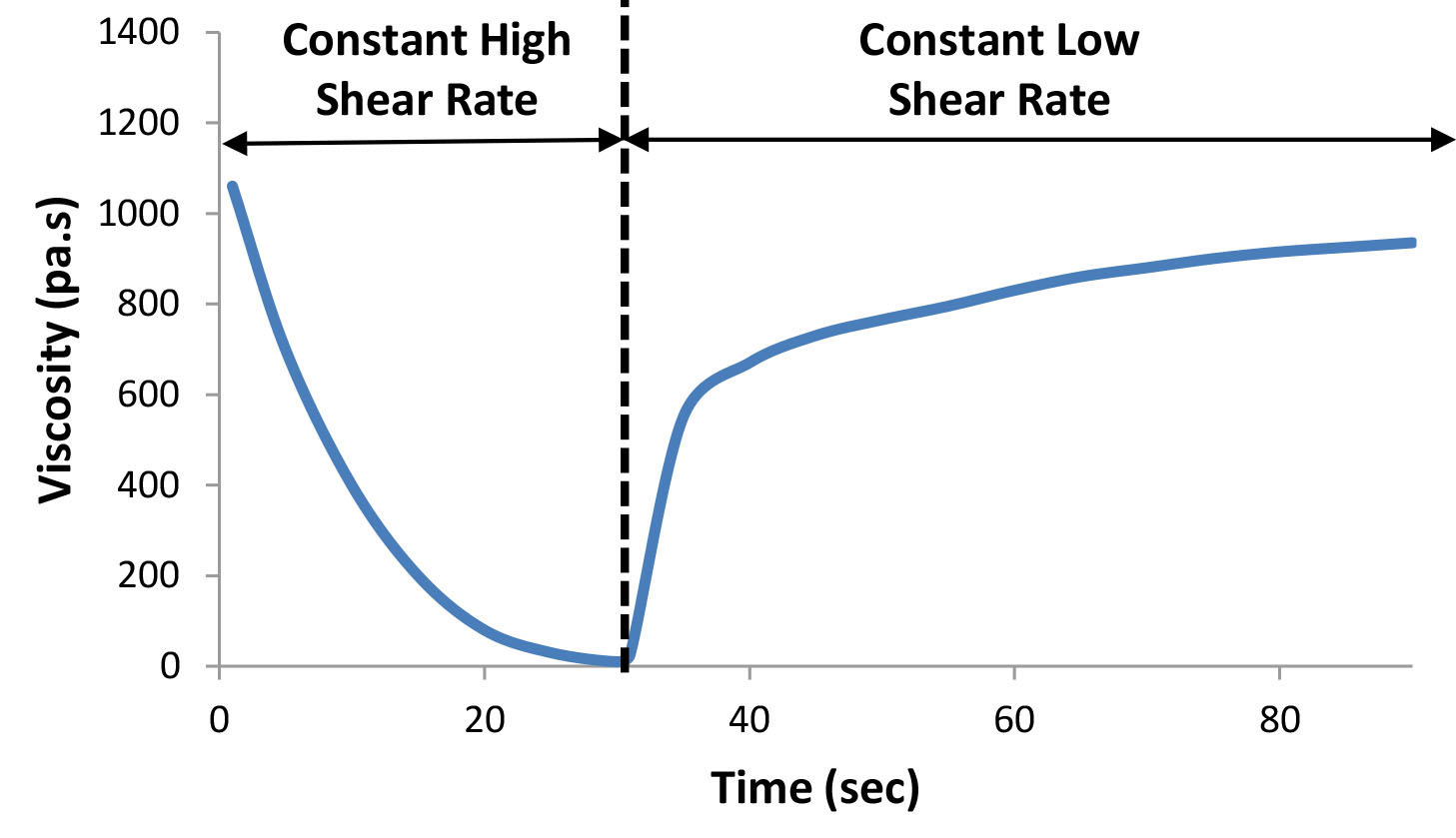
Figure 5: Viscosity as a function of time – shearing at a constant high shear rate (shear thinning), followed by shearing at a constant low shear rate (recovery).
It is important to recognize that the flow behavior of a complex fluid is best described by following its viscosity over a range of shear rates that represent the relevant application. Describing a system by a single number, representing "the viscosity” of the system would be adequate only if the system is Newtonian.
The flow behavior of a complex fluid also depends on the temperature and the pressure. The viscosity (η) usually (but not in all cases) depends on the temperature according to the Arrhenius relationship:
η = AeEa/RT
Where A is a constant, Ea is the activation energy, R is the gas constant, and T is the absolute temperature.
We can imagine an "elastic" system behaving like a spring, ideally regaining all of its initial energy when an external force is removed. A flowing, or "viscous" system would lose all of the initial energy when the external force is removed. However, most fluid systems exhibit a combination of elastic and viscous behavior. These fluids are named viscoelastic materials. We can calculate both the elastic component, the storage modulus (G’), and the viscous component, the loss modulus (G”), by a simple oscillation experiment. In a typical strain sweep test, the moduli (G’ and G”) are measured as a function of increasing strain at a constant oscillation frequency (see Figure 6). A characterization test in which the moduli are measured as a function of frequency, while maintaining a constant strain, is known as an oscillation sweep test (see Figure 7). These tests may indicate the relative elastic/viscous nature of the fluid, the breakdown process, and the strength of the inner structure of the fluid.
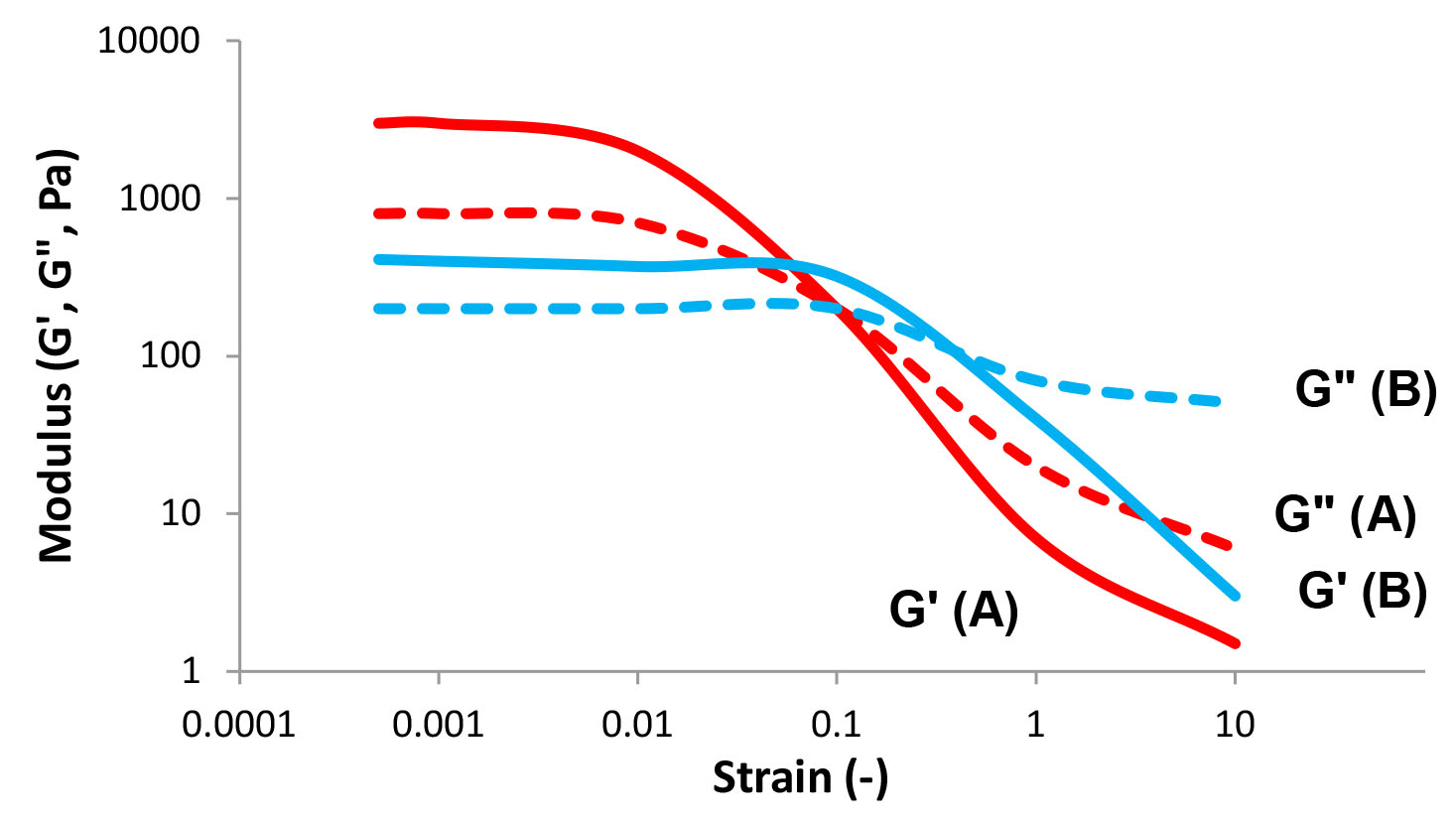
Figure 6: Strain sweep – storage (G') and loss (G") moduli as a function of strain at a constant frequency.
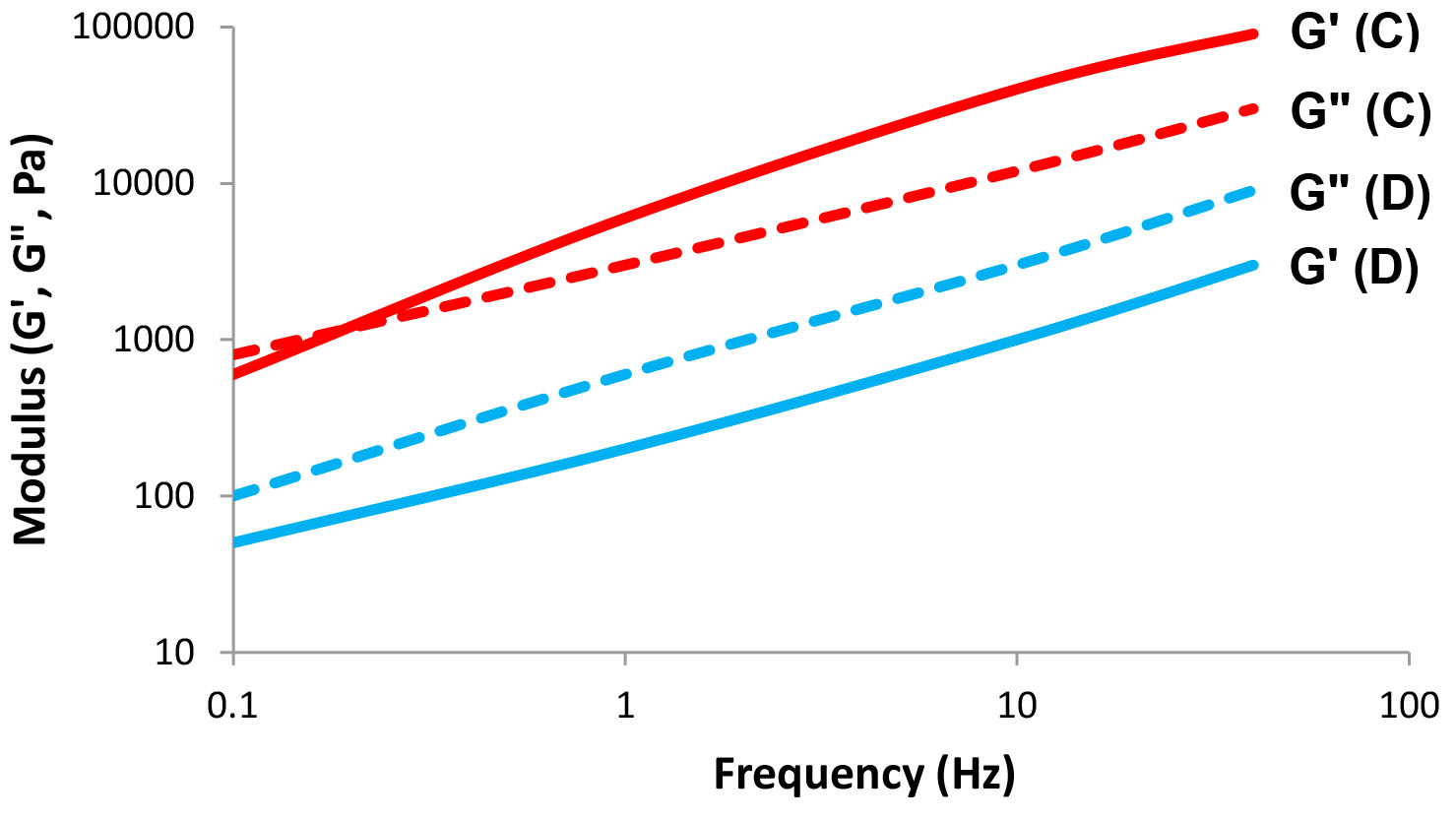
Figure 7: Frequency sweep – storage (G') and loss (G") moduli as a function of frequency at a constant strain.
A creep/recovery test is another way to characterize the rheological properties of complex systems. In this test, the change in strain (or compliance, which is defined as J = 1/G, where G is the Modulus) is measured as a function of time at a constant stress (see Figure 8). The test is performed in two parts: shearing at a constant stress over time, and then following the recovery after the stress has been removed. A creep test may provide information about the initial elastic response, shear rate at low stresses, the zero shear viscosity, percent elasticity, relaxation time, and the elastic modulus.
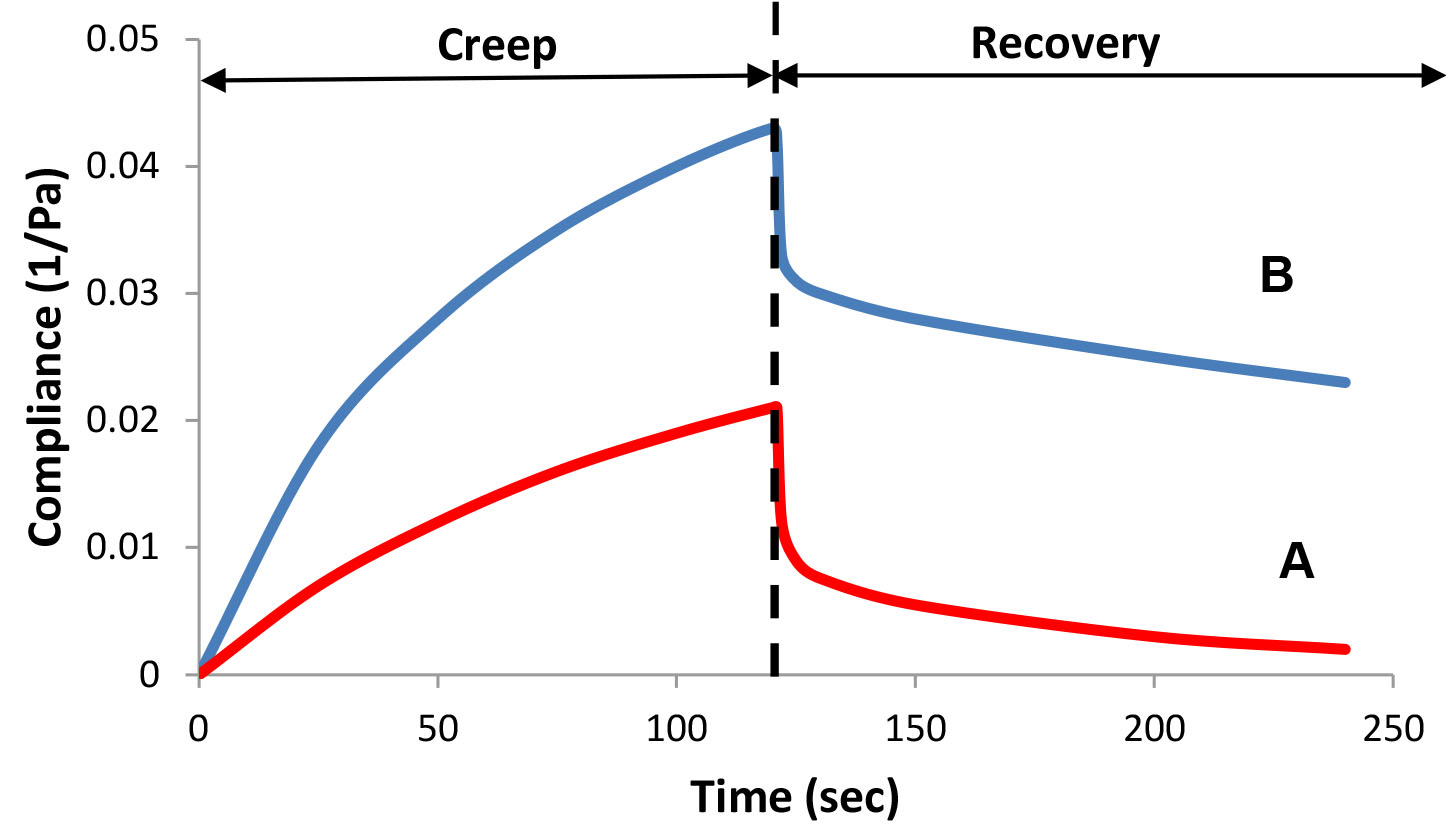
Figure 8: Creep/recovery test – compliance as a function of time.
Formulating products that exhibit optimal flow profiles requires the use of specific rheological additives that must be compatible with the system. The formulator may use combinations of thickeners to achieve the desired flow profile. Figure 9 shows how an “ideal” profile may be obtained by using two additives, one that exhibits high viscosity at low shear rate and low viscosity at high shear rates, while the second additive exhibits lower viscosity at low shear rate and higher viscosity at higher shear rates. Similarly, one may use a strain sweep, a frequency sweep, or a creep test to study the rheological properties of combinations of additives.
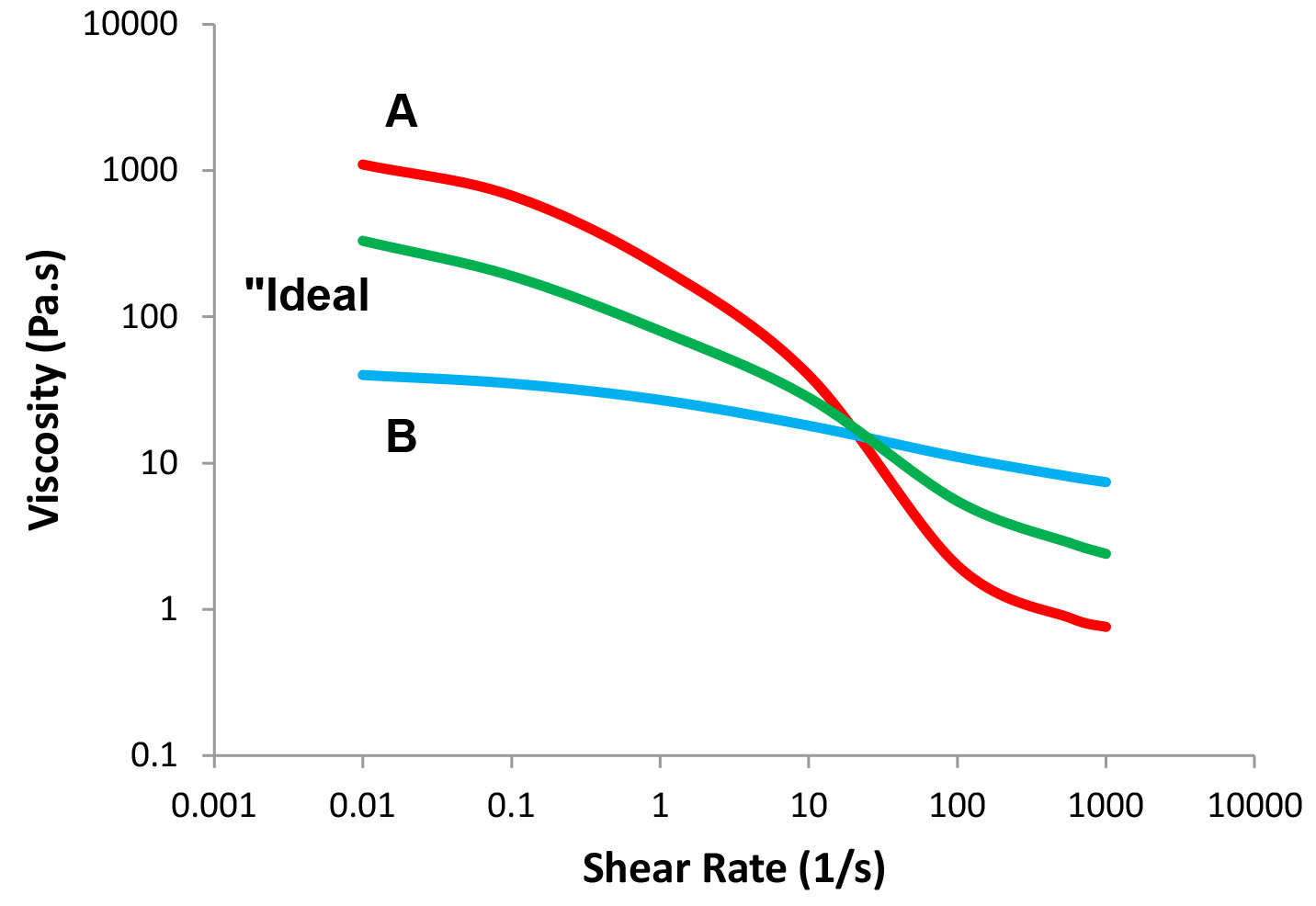
Figure 9: The "ideal" flow profile.
In many cases, combining two rheological additives does not necessarily result in a simple addition of their properties as implied in Figure 9. In many cases, the interactions between the additives may lead to a synergistic effect in which a blend of additives may impart an increase in the measured property, which is greater than the sum of the effects of the individual additives. Since we are dealing with complex fluid systems, the formulator should also explore the effects of additive concentration, cosolvents, surfactants, and salts as well as the effect of pH on the rheological properties of the formulation.
Understanding the basic principles of rheology and the rheological properties of complex fluids is critical to the development of an optimally successful cosmetic product. Characterization of the formulated product and studying the various rheological aspects of the formulation is an important part of the design of new and improved products and may shed light on the inner structure of the fluid during the different stages of its life cycle. Basic tests may include the flow behavior of the system—stress or viscosity as a function of changing shear rate, recovery of viscosity over time, determination of the yield value, thixotropy, creep/recovery behavior, and the effect of temperature. In addition, understanding the dynamic properties of the system may shed light on the viscoelastic nature of the fluid and its "elastic" and "viscous" behavior under stress and strain. These basic rheological attributes may provide the formulator with hints about the three-dimensional structure of the fluid and how to use the ingredients to formulate an optimal product. The above is just a simple description of the basics principles of rheology. Additional information on the principles of rheology may be found in many textbooks.5-12
1. M. Reiner, The Deborah number, Phys. Today, 17(1), 62 (1964).
2. D. Doraiswamy, The origins of rheology: A short historical excursion, Rheol. Bull., 71(1), 7-17 (2002).
3. I.S. Newton, Philosophiae Naturalis Principia Mathematica, 1st ed., Book 2, Section IX (1687).
4. R. Edgeworth, B.J. Dalton, and T. Parnell, Eur. J. Phys., 5(4), 198-200 (1984); http://smp.uq.edu.au/content/pitch-drop-experiment and http://en.wikipedia.org/wiki/Pitch_drop.
5. H.A. Barnes, J.F. Hutton, and K. Walters, An Introduction to Rheology, Elsevier Science: Amsterdam, Holland (1997).
6. F. A. Morrison, Understanding Rheology, Oxford University Press: New York, NY (2001).
7. C.W. Macosko, Rheology Principles, Measurements and Applications, VCH Publishers: New York, NY (1994).
8. D. Laba, Ed., Rheological Properties of Cosmetics and Toiletries, Cosmetic Science and Technology Series, Vol. 13, Marcel Dekker: New York, NY (1993).
9. H. Nae, Rheological Properties of Topical Formulations in Apply Topically: A Practical Guide to Formulating Topical Applications, N. Dayan, Ed. Allured Publishing Corporation: Carol Stream, IL (2013).
10. D.B. Braun and M.R. Rosen, Rheology Modifiers Handbook: Practical Use and Application, William Andrew Publishing: Norwich, NY (2008).
11. T.G. Mezger, The Rheology Handbook, Vincetz: Hanover, Germany (2006).
12. J. Mewis and N.J. Wagner, Colloidal Suspension Rheology, Cambridge University Press: Cambridge, UK (2013).