
Morphologically, hair is a composite material organized with a layer (or several layers) of flat cuticle cells wrapping an inner cortex comprised of elongated cortical cells. Clusters of cortical cells are maintained together by an extensive network of cellular membrane complex that surrounds each cortical cell. The cortical cells contain macrofibrils—roughly 200 nm diameter structures—that are comprised of smaller structures known as intermediate filament keratin proteins (IFKPs). At the inner core of the fiber, a vacuolated medulla exists and contains trace amounts of alpha-helical protein and lipids.1
Before we delve into the fine details of hair structure, we should clarify some nomenclature. IFKPs are often referred to as microfibrils, intermediate filaments (IF), or keratin intermediate filaments (KIF). In this article we will use the term IFKP. The IFKPs constitute the crystalline phase of the cortex and they are embedded in an amorphous matrix. The proteins that make up the matrix component of the cortex are referred to as intermediate filament associated proteins (IFAP) or keratin associated proteins (KAP). For the sake of clarity, we refer to these proteins as IFAPs.
Ultrafine Structure of Hair
X-ray diffraction (XRD) investigations of hair, carried out as early as the 1930s, consistently revealed a meridian reflection at 0.51 nm and an equatorial reflection at 0.98 nm (the meridian reflection is along the fiber axis while the equatorial reflection is perpendicular to it).1 These were the first hints of an ordered structure lying inside the hair fiber. Interpreting the results, Pauling et al. proposed the alpha-helix arrangement of the amino-acids constituting the secondary structure of hair: 18 amino acid residues in five turns, i.e. 3.6 amino acid residues per turn, form the alpha-helical chain, which is slightly coiled to account for the 0.51 nm meridian reflection (super-helix).3,4 Two super-helices combine to form a left-handed two-stranded rope-like assembly (coiled coil) in which the super-helices are arranged in such a way that the hydrophobic side groups at the outside of the helices interlink to form a stable “buttonhole” structure.5 These dimers are the actual structural subunits of the IFKPs, and are termed “molecular twins.” It should be noted that two coiled coil structures associate to form a protofilament, and two protofilament structures form a protofibril. An intermediate filament is actually composed of four protofibril structures.
Typically, a hair fiber is pictorialized as a protein-based layer (cuticle) wrapping a composite material made of inter-connected highly ordered IFKPs (containing the ordered alpha helices and often termed as “crystalline phase”) with less-ordered IFAP proteins (often termed as “amorphous phase”) and having a partly hollowed, protein-based core (medulla). For the sake of describing the behavior of the hair fiber, this image is casted into simplified physical models, generally named two- and three-phase models, which only describe the “crystalline” and “amorphous” phases, and sometimes also account for the inter-connecting region known as the “inter-phase.”6
The majority of proteins in hair are hard alpha keratins; fibrous proteins that contain a large amount of cystine, which account for approximately 21% mol of the total protein, as calculated from the sulfur content of gamma-keratose in human hair.7 This particular amino acid is capable of establishing disulfide bonds, resulting in cross-linking in the fiber, and provides the groundwork for most of hair’s physical and chemical properties. The disulfide bonds differ from other types of interactions within folded proteins, such as hydrogen bonds, electrostatic interactions, and van der Waals interactions, in that they are covalent and their stability is almost entirely dependent upon their environment.8
The nature of disulfide linkages in alpha keratins, at the level of fiber structural features, are often debated in the literature.9 While IFAP-IFAP, IFKP-IFKP, and IFKP-IFAP disulfide linkages are highly probable, intra-coil disulfide bridges, i.e., within a single alpha-helix, do not likely exist. Also, intra-rope disulfide bonds, i.e., between two alpha helices in the same rope, are unlikely to be present due to steric constraints. Overall, the disulfide bonds appear to contribute to the structure of the matrix and to what is termed in the three-phase model of keratin fibers as the interface region.10
Covalent and Non-covalent Bonds in Hair
Disulfide bonds are not the only types of bonds that cross-link proteins in hair. Salt bridges (ionic bonds or electrostatic interactions) and hydrogen bonds also contribute to hair fiber strength. Ionic bridges are difficult to quantify since they may occur between both charged amino acids (e.g., arginine and glutamine) and between traces of metals and carboxyl residues. Thus, they are usually not included in evaluations of hair fiber mechanics. Ionic bonds aside, the overall estimation of bonds in hair amounts to: 1 hydrogen bond and 1/9 disulfide bond per 122 g·mol-1, mean molecular weight of the keratin unit.11 The energetic values of the two types of bonds are:
1. hydrogen bond – 8-20 kJ·mol-1 (2-5 kcal·mol-1);
2. disulfide bond – 120-200 kJ·mol-1 (30-50 kcal·mol-1).
As a result, small mechanical effects could be related to the hydrogen bonds, while major mechanical properties are dominated by the presence of cystine.
Thus, the concept of hair mechanics may be grounded by the following statements:
1. Hair mechanics depend on the sum of disulfide bonds, hydrogen bonds, and ionic bonds; and
2.
While the hydrogen and ionic bonds may increase and/or decrease by changing ingredients of various hair treatments, disulfide bonds can only decrease during hair aging and harsh chemical treatments (e.g. permanent waving, relaxing, bleaching, etc.).
Taking these factors into consideration helps us explain the effect of moisture on the mechanics of hair. As water molecules enter the fiber, they tend to disrupt the hydrogen and ionic bonds, thereby diminishing the contribution of these bonds to the overall mechanical properties of the fiber. As a result, only disulfide bonds remain to respond to mechanical stimuli. When water is subsequently desorbed, the internal hydrogen and ionic bonds reform and the fiber recovers to its initial state.
Hair Mechanics
Hair mechanics is commonly evaluated by conducting tensile strength measurements, which provide data output in the form of stress-strain curves. Stress, usually reported in Pascals, equals the pulling force per cross-sectional area of the fiber (σ = F/A). Strain is typically reported as a percentage of the total fiber length and is the relative length variation of fiber under applied stress (ε = ΔL/L).
A typical stress-strain curve of hair has a sigmoid shape similar to that drawn in Figure 1 and is regarded to contain three regions related to the mechanically induced changes in the fiber. R1 is the linear elastic region, occurring at 2-5% strain, for which Hooke’s relationship holds: σ = E·ε (E being the Young’s modulus). R2 is the yield region, which appears like a slightly growing plateau beginning after the elastic region and ending at 25-30% strain. Finally, R3 is the post-yield region, which is up swinging from the yield region plateau and lasts to the breaking point (rupture of the fiber). The slopes of the straight lines drawn through most points of each of the three regions lie in a ratio of about 1:0.01:0.1 for most virgin fibers, pretty much independent of racial origin, when measured at 22 °C and 55% relative humidity.12
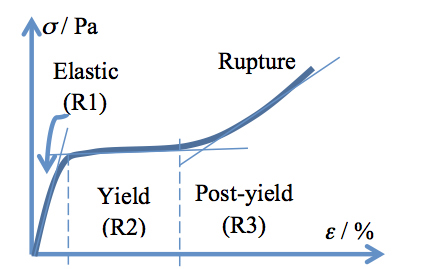
Figure 1: Stress-strain curve of a hair fiber with the three regions indicated. See the text for a complete description.
The hair fiber exhibits another interesting feature at stretching, namely the returning to the initial mechanic values if the stretching force is stopped (and the fiber is allowed to relax) prior to reaching the upswing point in the post-yield region. Carrying out such an experiment, one may generate a hysteresis curve, like the one provided in Figure 2. The integration of the areas below the recorded curves provides three values of energy: Wtotal, Welastic, and Wdissipated, respectively, characterizing the hysteresis loop.
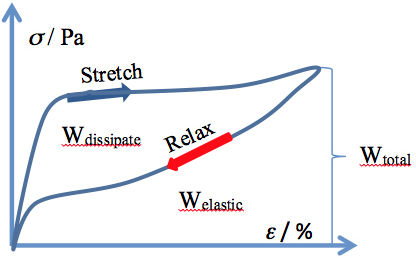
Figure 2:
Stress-strain hysteresis for a human hair fiber
The morphological structure discussed above and the curves illustrated in Figures 1 and 2, provide evidence that hair fiber is a viscoelastic composite material. XRD and Raman spectroscopy investigations of keratin fibers undergoing stretching demonstrated that the amount of alpha helix vanishes with increasing stretching, while the levels of beta sheet increases.13-15
Along with this information, and the knowledge of chemical bonds in hair, one may postulate on the succession of events that occur during stretching of the fiber. Within the R1 region (see Figure 1), the hydrogen bonds and some disulfide bridges break, enabling the freeing of alpha helices (IFKPs) inside the matrix (thereby suppressing contacts between IFKPs and IFAPs). This event is followed by the transition of alpha helices into beta sheets (changing the morphology of IFKPs) in the R2 region; and the subsequent extension of beta sheets and eventually their breakage, together with other disulfide bridges (which keep the IFKPs together), in the R3 region.
According to this model, hydrogen and ionic bonds only contribute to the value of Young’s modulus, while disulfide bonds and the amount of alpha helices dominate the overall mechanics. Derived from this interpretation, Young’s modulus of a hair fiber, Efiber, is the sum of Young’s modulus provided by each type of bond: Efiber = EH-bonds + Eionic bonds + Edisulfide bonds and, by measuring Young’s modulus of a fiber at different values of relative humidity (which affects hydrogen and ionic bonds), one may quantify the contribution of each type of bond to fiber elasticity.
Also a corollary of the model is that the area of the hysteresis loop (the dissipated energy, Wdissipated) relates to the number of alpha helices undergoing the transition to beta sheets:
Wdissipated = Wbreaking of H-bonds + Wα→β
Therefore, from the measurement of hysteresis carried out in the wet state (when hydrogen bonds are supposedly suppressed), one may evaluate the quantity of IFKPs, or more precisely the number of alpha helices or “crystallinity” of the fiber.
Insights from Thermal Analysis of Hair
Temperature also plays an important role in the behavior of hair since it is capable of acting on all the chemical bonds inside the fiber. Thermal analysis, particularly differential scanning calorimetry, DSC, is the tool used to explore temperature effects in hair. In agreement with terminology from polymer science, the IFKPs are called the “crystalline” region of the fiber and the target of DSC experiments is to detect the “melting” of this phase, and to evaluate the amount of IFKPs of the fiber from the value of the enthalpy of the process. Information on state of matrix, i.e. the IFAPs, is also available from DSC experiments since the melting behavior of IFKPs depends on the state of the surrounding matrix. To reiterate, the temperature at which “melting” of IFKPs occurs relates to the state of the surrounding IFAPs.
Two types of DSC experiment are typically carried out with hair fibers, dry-DSC or wet-DSC, using perforated or high-pressure crucible DSC pans, respectively. In dry-DSC experiments, the evolving gases during heating leave the system through perforations in the DSC pan. The result is a drying out of the fiber, making the matrix more rigid and keeping the IFKPs even firmer, which collapse only when the whole system collapses. In wet-DSC experiments, one uses hermetically closed pans in which water is added to the hair snippets before closing, and the pressure on the system inside increases while heating. In this manner, the matrix is softened quickly and IFKPs may denature earlier, before the collapse of the total system.
In both DSC experiments, one records an endothermic process (the temperature at which it occurs depends on whether a wet-DSC or dry-DSC experiment is conducted). This process, documented with XRD, is the thermal denaturation of alpha helices. However, neither in dry- nor in wet-DSC does the endothermic process corresponds to only thermal denaturing. The analysis of the two types of DSC experiments indicates that: a) during the dry-DSC experiment the endothermic peak is the result of competitive reactions of pyrolysis of the matrix and part of IFKPs, and the thermal denaturing of IFKPs; b) during the wet-DSC experiment the process is the result of a succession of reactions starting with the breaking of the bonds between IFKP and IFAP (particularly the breaking of disulfide bonds at this interface), followed by the thermal denaturing of the so-released alpha-helices of the IFKPs.16 Consequently the values of enthalpy, ΔH, recorded in the two DSC experiments are sums of these contributions:
ΔHdry-DSC = ΔHPyrolysis of IFAP and IFKP + ΔHThermal denaturation of IFKP
ΔHwet-DSC = ΔHBreaking of disulfide bonds at interface + ΔHThermal denaturation of IFKP
Concluding Remarks
In summary, IFKPs and IFAPs—along with disulfide, hydrogen, and ionic bonds—are the key structural elements in hair mechanical and thermal behavior and their quantification is of importance for evaluating the effects of cosmetic treatments. This appears to be a complex task since each experiment discloses only a facet of these elements.
References
1. C. Popescu and H. Höcker, Hair: The most sophisticated biological composite material, Chem. Soc. Rev., 36, 1282–1291 (2007).
2. W.T. Astbury and H.J. Woods, X-Ray studies of the structure of hair, wool and related fibres. II. The molecular structure and elastic properties of hair keratin, Phil. Trans. R. Soc. London, Ser. A, A232, 333-394 (1933).
3. L. Pauling, R.B. Corey, and H.R. Branson, The structure of proteins: two hydrogen-bonded helical configurations of the polypeptide chain, Proc. Natl. Acad. Sci. U.S.A., 37, 205-211 (1951).
4. F.H.C. Crick, Is α-Keratin a Coiled Coil?, Nature, 170, 882-883 (1952).
5. F.H.C. Crick and J.C. Kendrew, X-ray analysis and protein structure, Adv. Protein Chem., 12, 133-214 (1957).
6. J.W.S. Hearle, A critical review of the structural mechanics of wool and hair fibres, Int. J. Biol. Macromol., 27, 123–138 (2000).
7. C.R. Robbins, Chemical and Physical Behavior of Human Hair, 5th ed., Springer-Verlag, New York (2012).
8. T.E. Creighton, Disulfide bonds and protein stability, BioEssays, 8, 57-63 (1988).
9. R.D.B. Fraser, T.P. MacRae, L.G. Sparrow, and D.A.D. Parry, Disulfide bonding in alpha-keratin, Int. J. Biol. Macromol., 10, 106-112 (1988).
10. D. Istrate, C. Popescu, M. ErRafik, and M. Moeller, The effect of pH on the thermal stability of fibrous hard alpha-keratins, Polym. Deg. Stab., 98, 542-549 (2013).
11. R. Meredith, Rigidity, moisture and fiber structure, J. Text. Inst., 48, T163-T174 (1957).
12. C. Popescu, M. Istrate, and D. Istrate, unpublished results.
13. E.G. Bendit, A quantitative X-ray diffraction study of the alpha-beta transformation in wool keratin., Text. Res. J., 30, 547–555 (1960).
14. L. Kreplak, J. Doucet, P. Dumas, and F. Briki, New Aspects of the alpha-helix to beta-sheet transition in stretched hard alpha-keratin fibres, Biophys. J., 87, 640–647 (2004).
15. J.S. Church, G.L. Corino, and A.L. Woodhead, The effects of stretching on wool fibres as monitored by FT-Raman spectroscopy, J. Molec. Str., 440, 15-23 (1998).
16. C. Popescu and C. Gummer, DSC of human hair: a tool for claim support or incorrect data analysis? Int. J. Cosm. Sci., doi: 10.1111/ics.12306 (2016).